With the World Cup in full swing, I thought I’d try to tackle that age-old question: why do so many Americans hate soccer? Maybe if I can get to the bottom of that question, I can help some Americans find joy in the “beautiful game”…at least until World Cup 2014 is over.
First, a little context. I am an American who loves sports of all kinds but, I will admit, I hated soccer when I was younger. The reasons for this are many. I like to think that I’m typical in my soccer-aversion—typical of many other Americans—and this is what gives me some credibility in writing this blog post. But what’s interesting is that I eventually came to enjoy soccer, and it is partly the journey from hatred to enjoyment that I wish to share with you.
Why did I not like soccer? I can think of at least 4 reasons:
1) Turnovers. To an American immersed in the culture of American football (henceforth just called football) and basketball, it seems as though (in soccer) teams commit turnovers every five seconds or so. A little bit of background: a turnover (in any sport but soccer, really) occurs when one team gives up control of the ball. Normally, in most sports, a turnover is a major thing; statisticians keep track of turnovers, and the team that “turns the ball over” more loses most of the time. In basketball, a turnover often leads to a “fast break” (an exciting play usually leading to a score). In football, turnovers are catastrophic; fumbles and interceptions are often the most exciting plays in a game. They represent huge reversals of fortune. A football team which commits six turnovers in a game will almost always lose.
So imagine an American kid like me, watching soccer on TV for the first time (something that didn’t happen until I was almost in college, by the way). I see Spain playing Belgium in the World Cup. Spain has the ball…but within five seconds Belgium has the ball…but then within five seconds Spain has the ball…ad infinitum. An American football announcer could not possibly keep up: “Spain turns it over! Belgium kicks it…and turns it over! Now Spain has it but…oh no, they’ve turned it over! Belgium has a chance here…nice pass to Ceulemans…but he turns it over!” If you grew up watching football and basketball, this turnoverfest is maddening. It appears random, like pinball.
What I failed to realize, back in 1986, is that soccer is a game of averages, of field position, of drift velocity. It doesn’t really matter in soccer if the ball is “turned over” often. As long as (on average) the ball tends towards one end of the field or the other, one team will have an advantage.
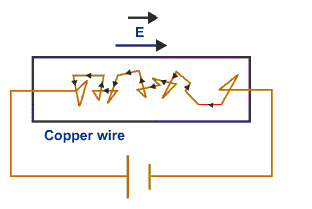
It’s like an electron in a copper wire, under the influence of an electric field: the motion of the electron is mostly random, but over time it tends to move in the opposite direction as E. If Brazil has a better team than Cameroon, then—despite the large number of apparent “turnovers”—the ball will tend to drift towards the Cameroonian goal. This drift velocity was apparent in the final stats from Monday: Brazil had the ball 54% of the time, and had 19 shots on goal (compared to 12).
I’ve learned to enjoy soccer, in part, by turning off my instinctual aversion to turnovers. When I watch soccer now, I am watching the semi-random kicking of an electron, which will tend (over time) to drift in one direction or the other, due to the superior ability of one of the teams. It’s a game of statistical mechanics; it’s irrelevant whether you keep the ball continuously for any particular length of time.
2) Low scoring. To an American used to basketball scores like 95-92, or football scores like 35-28, soccer seems boring, in part because scoring is so rare. But the “low scoring” of a soccer game should be taken in context.
For one thing, football isn’t as high scoring as you might think. The average number of points scored by American football teams in 2013 was 23.4. Consider that a touchdown (analogous to a goal in soccer) is worth a de facto 7 points (since the extra point is almost always successful). To compare football scoring to soccer scoring in any meaningful way, football scores should be normalized by dividing by 7. A score of 35-28 is analogous to a soccer score of 5-4. High scoring, sure, but not overly so. And a defensive battle like the Panthers/49’ers game last November, which ended with a Carolina victory of 10-9, is much like a soccer score of 1-1.
As for basketball, well, goals come so often that (individually) they lose almost all meaning. I like basketball, but a soccer goal is much more exciting for being so rare. Of course, it’s possible to make scoring too rare: I imagine that a game of Ullamaliztli was pretty boring indeed. You can only use your hips, and have to get a 9 pound ball into a tiny goal?
Which brings us to a tangential point. Basketball is a very pixillated sport, since the “quantum of scoring” (one point) is so meaningless. In soccer, the quantum of scoring (one goal) is a much, much bigger deal. This makes soccer goals more entertaining, on a 1-1 basis, than basketball goals; but it also means that you’re measuring the worth of individual teams with a very blunt instrument. A football victory, 10-9, becomes a draw in soccer (when normalized) because the goals are not finely-tuned enough to “detect” a difference in such evenly matched teams. Whether this is a good thing or not is up to debate.
3) Red cards. To an American, penalties are a common and necessary part of having a physical game. But in soccer, the penalties seem very out of proportion to the offenses committed.
Consider a tackle in soccer. It’s OK to tackle the opponent if I get my foot on the ball. But if I miss the ball, I’m going to get penalized. And if the referee thinks that I was trying to trip the opponent on purpose (a very subjective thing), I’ll get a yellow card waved in my face. Two yellow cards equals a red card, and I’m out…and my team is now down one player.
Seriously? Down one player for the entire game?
The same thing happens in ice hockey. It’s called a power play. And when the other team scores, the penalized team gets the player back. The power play ends, and everything is fair again. Why can’t it be like that in soccer?
I’ve always felt that your entire team losing a player for the rest of the game should be the nuclear option of penalties, such as if one of your players bites another on the shoulder. It shouldn’t be used against a player that commits two ticky-tack penalties. This is especially true in an era when diving (called flopping in the USA) has become a cottage industry. Why not dive, when you have a good chance of ejecting a player from the game entirely?
In football, you have to do something egregious to get tossed out of a game, like throwing a punch. Even then, your team is not down a player; a substitution is allowed. In NBA basketball, you can commit up to 5 personal fouls; you’re tossed out on the 6th (this is called “fouling out”). Again, when you foul out, your team isn’t penalized unduly…they put in someone else to take your place.
How does an American learn to accept the harshness of the red card system?
With difficulty, I admit. I still don’t like it. But I sort of understand it. After all, how else can you penalize a team in a game in which there’s no stopping of the clock? If players were allowed five, or four, or even three yellow cards before being tossed out, I daresay there would be more tripping, more pushing, more dangerous plays…and more injuries. Then again, there would be less diving…
4) Offside. This might be the hardest aspect of soccer to fathom, to a person raised on Michael Jordan fast breaks and Dan Flutie Hail Mary passes. Why do you penalize a team for having a player in scoring position? Get rid of the offside penalty (the idea goes) and scoring would go up, and the number of exciting plays would increase.
Oh, who am I kidding. I still hate the offside rule.
“But wait!” the soccer aficionado says. “You get rid of offside penalties, and people will just park in the goal, waiting for a ball. What’s the excitement of that?”
Um, that happens already. It’s called a corner kick. And corner kicks are exciting.
Sure it would change the game. There would be no more beautiful offside traps. Instead, there would be fast breaks. Which is more likely to end up on a highlight reel: a well-executed offside trap, or a well-executed fast break? I’ll let you decide.
Which brings me to soccer’s flaws (yes, it has flaws, just like every game and sport does.) Not only should the offside rule be tossed out (or at least relaxed), but shootouts to decide a game are ridiculous. Why? Consider that a shootout contest has little relation to the actual game of soccer. It is, if you will, a different (but related) sport entirely. Settling a game with a shootout is like settling a basketball game with a free-throw shooting contest. Why anyone thinks that shootouts are a good idea is anyone’s guess. Sure, they can be exciting…but settling a soccer game with a spin of the roulette wheel would be “exciting” too—that doesn’t mean we should actually do it. Just have extra periods until someone scores a golden goal. And if you’re concerned with players getting too tired, well…there are a lot of players sitting over on that bench. Don’t you think some of them would like a chance to play?
Ultimately, I like soccer, despite its flaws. I’ve gotten used to the offside rule; I recognize it as a rule that purposely rewards passing and open-field play, at the expense of shots-on-goal. It’s a choice, to make soccer a particular kind of game, no better or no worse than the (different) game you’d get without the rule. Similarly, I’ve learned to embrace the shootout: they are rare, after all, and only occur after an extra period has failed to designate a winner. In such a case, the teams are so evenly matched that we might as well use a flip of the coin. And we’ll call that coin flip a shootout.
Note: I’ve made no mention of baseball in this discussion. The reason? Come on. Baseball is just boring.
*********************************************************************************************
If you enjoyed this post, you may also enjoy my book Why Is There Anything? which is available for the Kindle on Amazon.com.
I am also currently collaborating on a multi-volume novel of speculative hard science fiction and futuristic deep-space horror called Sargasso Nova. Publication of the first installment will be January 2015; further details will be released on Facebook, Twitter, or via email: SargassoNova (at) gmail.com.