Winston Churchill and Violet Bonham Carter now appearing in: Many Worlds Comix #4!
Posted in Comix | Tagged Bryan Smith, Churchill the cat, Edward Cantasano, Helena Bonham Carter, Matt Damon, Stephen King, Violet Beauregarde, Violet Bonham Carter, Winston Churchill | Leave a Comment »
Imagine that there’s an ice cream truck parked near a school. It’s 3pm; class is dismissed and a steady stream of kids approach the truck. For simplicity, let’s stipulate the following rules:
1. If a kid has enough money, he or she will buy an ice cream cone;
2. A kid will only buy one ice cream cone;
3. A kid will buy the most expensive ice cream cone he or she can.
After the kids buy ice cream (or not) they continue on their way, having whatever leftover money they might have in their pocket.
My question is this: by seeing how much money kids have left, what can you determine about the prices of ice cream cones? (Astute observers will note that this toy model has many similarities to the Franck-Hertz experiment of 1914, but we’re not there yet.)
Let’s look first at some hypothetical data. Here we have plotted L (money left over in a kid’s pocket) as a function of M (how much money a kid started with) for a school with 11 kids:
There doesn’t seem to be a pattern. Maybe we don’t have enough data? Let’s increase the number of kids to 42:
The sawtooth form of the function is characteristic of problems of this type, and can be understood intuitively. First of all, notice that the function is linear to begin with, with a slope of exactly one; this means that below a certain threshold value of M, a kid can’t afford any ice cream, so he/she ends up with the same amount of money he/she started with. Eventually, if M ≥ $1, a kid can buy a cone; L then plummets because the kid has spent a dollar.
It seems obvious from the graph, then, that ice cream cones are priced at $1, $2, and $3; beyond that we don’t have any data so can’t draw more conclusions.
Now, if we relax the stipulation that kids only buy one cone, then our data is ambiguous. Maybe the cones are priced $1/$2/$3, or maybe cones are always just $1, and kids are buying more than one cone if they can. We can’t distinguish between these cases; that’s why I put the original stipulation there to begin with.
Let’s try a more challenging graph:
This graph is much harder to interpret. The first peak is much bigger than the others; there is also a very tiny peak on the right-hand side. It helps if you know where the jumps are: L jumps down to zero whenever M is equal to $0.67, $1.02, $1.34, $1.69, $2.01, and $2.04. If you want to work out the ice cream cone prices for yourself, feel free. I’ll wait.
The solution? A little trial and error will give you two different prices for ice cream cones: A= $0.67 and B=$1.02. Then the jumps occur at A, B, 2A, A+B, 3A, and 2B. If we were doing physics, we’d make a prediction: we would expect the next jump to occur at $2.36, which is B+2A. Observing this would support our hypothesis. But if the next jump occurred at $2.22, say, then we’d have to revise our theory and posit a new ice cream C priced at $2.22.
What does any of this have to do with physics?
I use this example when I introduce the Franck-Hertz experiment to my students. This experiment was first performed in 1914 (an auspicious year!) and provided support for Bohr’s idea that atoms have specific (quantized) energy levels. Electrons are accelerated and shot towards mercury atoms (in a vapor). The electrons may then give energy to the atoms (exciting them) or they may not, bouncing off without loss of kinetic energy. We look at how much energy the electrons have to start with, and how much they end up with, and thereby deduce the energy levels of the mercury atoms.
How is that possible? In terms of the analogy, make the following transformations:
kids –> electrons
ice cream truck –> Hg atoms
kids buying ice cream at certain prices –> electrons giving certain amount of energy to Hg atoms
prices of ice cream cones –> energy levels of Hg
M (initial amount of money) –> V (proportional to initial kinetic energy of electron)
L (leftover money) –> I (proportional to final kinetic energy of electron)
If energy levels of an atom are truly quantized, then we would expect a graph of I vs. V to look like our graphs above, with an increasing sawtooth pattern. Where the drops occur will then tell us the specific energy levels of the Hg atom. (Incidentally, why do we use V and I? Well, in the actual experiment the easiest way to measure initial kinetic energy is by measuring the voltage used to accelerate the electrons; the easiest way to measure final kinetic energy is to measure the current of the electrons after they have passed through the Hg vapor.)
How did the experiment go? Here are the results:
It should be obvious that atomic energy levels have specific “prices”, and that there’s a minimum amount of energy that an electron must have in order to “buy” an atomic transition (exciting the atom at the expense of the electron’s kinetic energy). It remains for the experimenter to do some elementary unit conversions, to translate I and V into final and initial kinetic energy.
[Note for advanced students and/or physicists: it is interesting to ponder the following questions, which highlight the fact that the ice cream analogy is not perfect: (1) why is the I vs.V graph not linear at low voltage? (2) After “spending” kinetic energy to cause the first excited state, why does the electron’s energy not drop all the way down to zero?]
Posted in Physics | Tagged Franck-Hertz, Physics, physics instruction | 6 Comments »
CNN recently posted a story about how the Feb. 15 asteroid/meteor event was very, very unlikely: a 1 in 100,000,000 coincidence. I disagreed. I was all ready to blog about how CNN, yet again, got a non-scientist to write about science…and my indignation was already half out of the bottle.
Then I saw who wrote the article: Meg Urry, a highly respected Yale astrophysicist.
So, I sat on my hands for a second and re-evaluated the article. It does not contain any errors as far as I can tell. But I still contend that the article is misleading: saying that the asteroid/meteor event was a 1 in 100,000,000 coincidence is the wrong way to look at it.
I agree that if you multiply 1 in 3,650 days times 1 in 36,500 days you get something close to 1 in 100,000,000. But all you’ve proven is that for any given random day, there is only a 1 in 100,000,000 chance of such a coincidence occurring.
However, we now live in a post-Nate Silver, post Bayesian controversy world, right? We’ve known about asteroid DA14 for exactly a year (as of today). So the right question to ask, before it flew by last week, was: what is the chance that a human-injuring meteor will fly by on the same day? Well, given that an asteroid will already pass that day, the chance of a once-in-a-decade meteor flying by that same day is just 1 in 3,650 (that is, once in a decade).
I have the utmost respect for Dr. Urry. I suspect that the hyperbole-filled title of her CNN post was written by a CNN webmaster, not her. I still agree that the coincidence was unlikely, but given that DA14 was already expected to fly by, the Chelyabinsk meteor hitting on the same day does not sink into the realm of unbelievability.
[Trivia note: Chelyabinsk is the birthplace of Evgeny Sveshnikov, the chess grandmaster for whom the Sveshnikov variation of the Sicilian defense is named. And I do know that, as much as I like the Sveshnikov defense, I tend to go down in flames like a meteor whenever I play it.]
Posted in Physics, Rant | Tagged asteroid DA14, Chelyabinsk meteor, Nate Silver, statistics, Sveshnikov | Leave a Comment »
The following is a list of foods I love today, at the age of 44. I can’t imagine the 10-year-old me even trying any of these foods, much less liking them. But we grow up; our tastes change, and hardly a day goes by without me craving Marmite. I mean, come on? Isn’t that weird? Please tell me I’m not crazy!
10. Fresh spinach
I didn’t really learn to enjoy salads all that much until I discovered that fresh spinach is infinitely tastier than lettuce. As a kid, I think I tried spinach, in a can, like Popeye; the problem is, canned spinach is barely edible. When you eat a fresh spinach salad, maybe with apples and a splash of bacon vinaigrette, you can only wonder: is this really the same plant as found in canned spinach? Hard to believe.
9. Snails
I’ll be honest; I’ve only had snails (at most) 10 times in my life, and always in a fancy restaurant. But they’re tasty. They taste even better when you call them snails, since calling them escargot leaves a bit of a snooty aftertaste.
8.Soft-shelled crab
I first tried this in a Thai curry dish. I still find the texture a bit strange, but overall I find the taste delectable.
7. Mushrooms
I’ve liked mushrooms for a long time, but can’t recall whether I tried them as a kid or not. I think most Americans are first exposed to mushrooms as a topping on pizza, but I don’t really like mushrooms that way. They invariably go straight from a can to the pizza. Fresh mushrooms are better, and stuffed mushrooms may be the best of all. As a bonus, there are many, many varieties, and they all taste different.
6. Mortadella
To my mind, mortadella is the king of sandwich meats. It’s a bit like deli bologna, but more flavorful: it is marbled with pork fat, and often has pistachios and olives mixed in. I might have liked this as a kid, but I never tried it. I had never even heard of it. I’d have to drive over a hour from where I live to find this today.
5. Runny eggs
Yolk freaks kids out. But not me. Over-easy is the way to go. And when the Hollandaise in an Eggs Benedict runs together with the yolks…
4. Coffee
I guess I haven’t grown up entirely. I don’t drink coffee, unless it’s cold with plenty of milk and sugar. Sort of like a melted coffee ice cream. My favorite way to have coffee is the way they serve it in the Vietnamese restaurants: over ice, with sweetened condensed milk.
3. Pomegranate juice
So bitter. Yet so good somehow. I don’t really know why I like it.
2. Stilton
The king of cheeses. Radically strong flavor; almost hallucinogenic. Not just for Wallace and Gromit anymore.
1. Marmite
What can I say? Marmite, objectively, doesn’t taste all that great: it’s almost pure umami, like chewing on a bouillon cube. And yet it is alluring for some unfathomable reason. On bread, with butter, it is divine; mixed with honey and corn syrup, it is the ideal pizza sauce. I can get Marmite (or its complex conjugate, Vegemite) where I live, but I don’t eat it all that often. I may go 6 months without having any. Then, on a random day…the 19th of February, say…I will start to crave it, and even start to blog about it.
Posted in Uncategorized | Tagged Foods kids hate, Marmite, mortadella, mushrooms, pomegranate juice, runny eggs, snails, soft-shelled crab, spinach, Stilton, Vietnamese coffee | 6 Comments »
In the 1985 film Young Sherlock Holmes, Holmes tells Watson the following riddle: “You’re sitting in a room with an all-southern view. Suddenly, a bear walks by the window. What colour is the bear?” (He says “colour” not “color” because he’s from the UK.) As I recall it takes Watson most of the movie to give the obvious answer—white—because the bear must be a polar bear. All southern view…North Pole…polar bear…you get the idea.
Over the years I’ve hear other versions of this riddle. The most common seems to go something like this: “A hunter travels a mile south, a mile east, shoots a bear, then travels a mile north to her starting point. What color was the bear?” People assume that this riddle is isomorphic to the previous one, because (supposedly) there is only one place on Earth you can travel the same distance south, then east, then north, and return to the beginning. But this is wrong. There are an infinite number of places on Earth you can travel in a loop that is 1 mile south, then 1 mile east, then 1 mile north.
Of course, starting at the North Pole is one solution. But there are also many, many more solutions close to the South Pole. Imagine, for example, a latitude roughly 1/(2π) miles north of the South Pole; in such a case the parallel along that latitude is the circumference of a circle, given by
C = 2πr = 2π [1/(2π)] = 1 mile.
(I said roughly because we’re on the surface of a sphere, so the circumference of a parallel is not exactly 2πr—because r is an arc length, not a straight line—but 1 mile is so much smaller than the radius of the Earth that we can assume a locally flat geometry.) If a hunter started his journey 1 mile north of this latitude, then of course he could go 1 mile south, then 1 mile east (circumnavigating the South Pole!) and then 1 mile north, and return to his starting point; I presume there would be no bears.
There are actually infinitely many solutions that work. In each case, after going a mile south, the hunter would have to reach a latitude in which the circumference C was an integer fraction of 1 mile. That is, it must be true that
C = 1/n miles,
where n is an integer. This means that the parallel would have to be
r = C/(2π) = 1/(2πn)
miles from the South Pole (again, this is a flat approximation to a spherical problem). So the most general South Pole solution is that the hunter should begin 1 + 1/(2πn) miles north of the South Pole. For example, take n = 5. If a hunter starts 1.0318 miles from the South Pole, she can go south 1 mile, east 1 mile (circumnavigating the South Pole exactly 5 times) then north 1 mile, and relax in her hot tub. No bears will be harmed, unless some evil genius has released them in Antarctica.
The original version of the riddle, as given by the young Sherlock Holmes, is superior, since it has only one solution. We can conclude that Sherlock Holmes was good at math.
I mean, maths.
Posted in Uncategorized | Tagged maths, Polar bear riddle, spherical geometry, Young Sherlock Holmes | 11 Comments »
One day in the summer of 2011, while mowing the lawn, I saw a strange creature flying through the air.
Actually, “flying” is too generous a term. The creature was lilting through the air. Lurching. It appeared to have ten legs, and was about the size of a silver dollar. I was puzzled, to say the least, but that lawn wasn’t going to mow itself so I went back to work.
I live in a rural area in the mountains of North Carolina, only 30 minutes away from the entrance to the Great Smoky Mountains National Park. There’s a lot of wildlife here: I’ve seen bear, elk, deer, raccoons, opossums, groundhogs, voles, and squirrels; our bird feeders are always full of cardinals, chickadees, towhees, finches, and titmice; and I once came home to a 4-foot black snake inside my house. As for arthropods, I’m very familiar with flies, no-see-ums (family Ceratopogonidae), moths, wasps, honeybees, crickets, ants, beetles, and spiders of all kinds. I’ve had close encounters with black widow spiders no less than 3 times in my life.
But this thing? With 10 legs? Lurching through the air like a drunken hang glider? Incomprehensible.
Over the course of that summer, I saw such creatures on numerous occasions. I gradually came to realize that they were insects, since subsequent sightings showed 6 legs, not 10. My working hypothesis was that what I saw that first day was a mating pair: two of these things stuck together. But I still had no idea what the confounded creatures were.
In appearance, the insects were bizarre to say the least. They were striped, like zebras, and their legs appeared to have at least 3 joints each, so that the legs took on a zigzag character. They didn’t appear to use their wings, which I guessed were vestigial; rather, picture a 6-legged starfish up on one end, clawing and grasping its way forward. As a physicist, it looked very much like the creatures were literally swimming through the air. And so I resolved, with the help of the internet, to positively identify them.
Rutherford said that “all science is either physics or stamp collecting.” A lot of people take this to be a disparaging comment about sciences other than physics, but I don’t. I kind of like stamp collecting. I like being meticulous, and being detailed. That’s why I like pastimes such as putting together 1000-piece puzzles.
But my search for the identity of the “mystery bug” took stamp collecting to a whole new level. It literally took me a month of sleuthing to identify the things. I tried the obvious first: I googled things like “strange zebra striped bug” and “bug that swims in the air” but had no luck. I posted a question on an entomology bulletin board. I looked at websites dedicated to “insects of the Appalachians.”
Finally, I had a breakthrough: I saw one of the bugs hitting up against a window in our house. For the first time, I could see the creature close up and for more than just a second or two. I verified that the creature did have six legs; I verified that it did have wings, although they seemed useless. I realized that my mystery bug was a crane fly. Here’s a more typical, run-of-the-mill crane fly:
Regular crane flies are common where I live; kids often mistake them for gigantic mosquitoes (which they are not).
Once I realized that the mystery bug was a type of crane fly, my task was eased enormously. And eventually I found this assortment of photographs. Eureka! I had done it! They were phantom crane flies, of the family Ptychopteridae. Specifically, they were the species Bittacomorpha clavipes, which, according to this Wikipedia article, are “known for the odd habit of spreading out [their] legs while flying, using expanded, trachea-rich tarsi to waft along on air currents.”
It turns out that the phantom crane fly is one of the very, very few creatures on Earth that fly without using their wings. They are literally swimming, somehow taking advantage of a high Reynolds number (let’s say, 265?) to sludge through the atmosphere without those wings that evolution gave them. Consequently they look more like seed pods drifting on the wind than they do insects.
What is my point? I don’t have one. I just think these bugs are cool, and you should try to find them if you ever visit the Eastern United States. They hang out in marshy areas in late summer. Oh, and if you’re a physicist or an entomologist, think about studying these little guys. The field’s wide open as far as I can tell. Somebody needs to video the flight of the phantom crane fly, so get on it! [Note added later: I did find this video which shows the weird flight, are there more?]
Posted in Uncategorized | Tagged entomology, insects, phantom crane fly, Physics, physics of flight, Rutherford, science | 20 Comments »
There is a principle in physics which says that, essentially, if two things are entirely indistinguishable, then you might as well call them the same thing. There is even a branch of statistics (Bose-Einstein statistics) which is based on this principle.
Now, the meaning of the word “indistinguishable” has a very specific meaning in this context. In physics, two things are indistinguishable if they cannot be distinguished no matter what anyone does. That is, they cannot be told apart even in principle. If there is a way to tell two things apart, then “regular” statistics holds; but if they truly are indistinguishable then they obey the much less intuitive Bose-Einstein statistics mentioned previously.
(As an aside, and entirely as a speculative exercise, one could argue that the existence of particles which clearly do obey Bose-Einstein statistics means that either (1) there is no God, or (2) there are things that even God cannot do—such as distinguish such particles—because if God could distinguish them then why do they obey Bose-Einstein statistics in the first place? But that sounds like an idea for a later blog post…)
As an example, suppose a photon is absorbed by an atom, and the atom subsequently emits another photon of the exact same frequency and polarization. One could say that a photon was absorbed and then the same photon was re-emitted; or one could say that a photon was absorbed (and destroyed) and then a completely different but identical photon was emitted. The principle of identical particles says that these two cases are equivalent. Neither one is right, or wrong. Whichever you choose to believe is a matter of taste. There is no experiment that even God could do that would tell you which was “right” and which was “wrong”, so why worry about it? They represent the same thing.
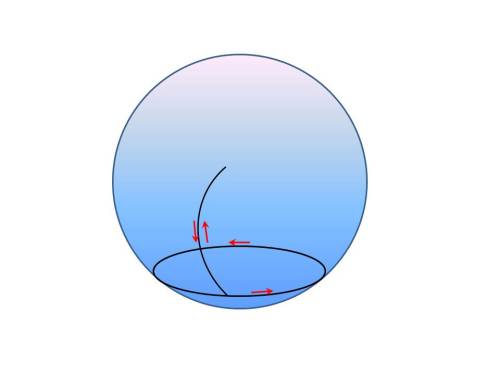
Suppose two identical particles interact. Initially they are traveling South and East, respectively, and interact at the origin:
We can’t see what “actually” happens at the origin. After the collision they are traveling South and East again. If that’s all you know, and all you could know, then which of the following cases is correct?
Case 1. They passed right through each other without actually interacting:
Case 2. They each turned 90° and switched roles, so to speak:
A physicist would say that these are identical situations, as long as no one, not even God, is allowed to look under the veil. And the distinction isn’t just semantic: if the particles are distinguishable, and these two cases really do represent two distinct physical possibilities, then the statistics of what we observe in such situations will be different.
Now, what in the world does this have to do with philosophy?
I’ve often felt that philosophy could stand to have a similar principle. Well, fine, let’s just do it. Let’s just make the following hypothesis:
If two things are indistinguishable even in principle, then they are the same.
Now I’d like to apply this principle to what I call the “Next morning” paradox but which is virtually identical to the Swampman paradox of Donald Davidson. Suppose I go to sleep tonight and enter a deep sleep (so that I am not even dreaming). And suppose that during this time of unconsciousness my body spontaneously disintegrates, and just happens to be replaced with an identical one: identical in every way, including the position of every molecule. (Of course, you might try to cite Heisenberg here and say you could never make a body exactly like a previous one, because there’s always some uncertainty in position and/or momentum. But, as in the original Swampman example, we assume that luck prevails: just by random chance the atoms are all found in the same way.) This new version of “me” wakes up, lives his life, and no one (not even the new me) has any idea that anything has transpired.
Davidson and others contend that the new me is not “me” at all, even though no one could tell the difference. They say that there is some intangible spark that can never be quantified that somehow still distinguishes yesterday’s me and today’s me. That is, the difference between the two me’s is magic. I find this ludicrous.
Any being that has all of your physical properties, and more importantly, all of your mental properties and memories, is you. This may bother some, because it implies that more than one “me” can exist simultaneously; after all, we could make an exact replica of me and leave the old me intact. Well, who cares? As a many worlds adherent, I guess it’s not surprising I wouldn’t be bothered by such a scenario at all.
I find these ideas so obvious that it’s almost difficult for me to convey the ideas without screaming internally. The principle has its beginnings in physics, but I find it applicable here: if x and y are indistinguishable even in principle, then x = y. End of story. I frankly have no idea why anyone takes Davidson’s ideas seriously anymore.
Think of it this way: suppose you knew you were going to be killed, but that an exact replica of you would be put in your place, and have all your memories, and live your life. On a visceral level, you’d probably be upset: “you” would live on, but it wouldn’t really be “you”. This is the developmental stage that Davidson is stuck in.
My response: that scenario might have happened last night. You might actually have died, and been replaced. No big deal, right? In fact, it might be true that everyone dies, every single night, and is always replaced by a perfect simulacrum. The important point is that you could never know. No one would know. The universe would appear exactly the same. We might as well take these two cases (that we are replaced, or that we are not) as being operationally identical. For all intents and purposes, you can assume that every night you die, and that in the morning a different version of you is created with the same memories, that will act exactly as you would have acted. Because this way of looking at things is really identical to the way we normally perceive reality, there can be no harm in thinking this way. In fact, thinking this way may very well lead to insights and attitudes that you wouldn’t have had before.
I find this idea strangely liberating. Each “me”, every day, can be thought of as a different person, related to me, and sharing some of my qualities, but separated both by time and space. And we’ve come now to the final point of this post: how I learned to stop procrastinating. For when you think of future selves as being entirely different people (which, in some sense, they are) then you can start thinking about doing favors for your future selves.
I don’t want to clean the kitchen now. I could procrastinate. However, to do so would be doing a disservice to “future me.” Why not clean the kitchen today, and do a favor to my future self? It’s no different than doing the dishes as a favor to your spouse, or mowing a lawn as a favor to a friend. Your future self will appreciate it, and be grateful for your thoughtfulness.
For, if you’re a nice person, and enjoy helping others, why not put your future self in that category? Treat your future self as a fully formed, thinking, rational person, with thoughts and feelings and aspirations and concerns. It’s easier to do this if you actually think of a future self as a different person entirely. Then, it will be easier to do a favor for this person, be nice to them, care for them, sacrifice for them. When seen in this light, procrastination is just a form of selfishness. Would you get drunk if you knew someone else, a random person somewhere, would have a terrible hangover because of your actions? I’d hope that most people would not. And yet, “Saturday morning you” is a person, just like “Friday night you” is. So why be so selfish? Why have that tequila?
I am not trained as a philosopher, although I have published works on the philosophy of quantum mechanics. Nevertheless, I don’t think philosophy is the exclusive playground of those with philosophy PhD’s. As this example shows, something as abstract as Bose-Einstein statistics can inform “traditional” philosophical questions such as the existence of God, the mind/brain problem, and philosophical zombies. My intent here is to get people thinking, discussing, evaluating. Science and philosophy are not enemies. They’re frenemies. Let’s hope they continue to play together in the sandbox.
Posted in Many-worlds Interpretation | Tagged Bose-Einstein statistics, identical particles, many-worlds, philosophical zombies, philosophy, procrastination, Swampman | 7 Comments »
What do the colors pink, gray, and beige have in common?
For one thing, they’re all annoying. I mean, come on…this isn’t rocket science.
But why are they annoying? Why is lilac (RGB = [220, 208, 255]) so insipid? Why does jasmine (RGB = [248, 222, 126]) make one vaguely nauseated? Why is Crayola fuchsia (RGB = [193, 84, 193]) worse than a bout of the common cold? (Use this applet to investigate these combinations.)
My thesis is this: that these colors are so annoying because they’re extra spectral colors. And on some primal, instinctual level, humans don’t like extra spectral colors very much.
In a previous post, I talked about how humans have 3 kinds of cones in their retinas. Roughly speaking, these cones react most strongly with light in the red, green, and blue parts of the visible spectrum. Now, as I mentioned, “color” is a word we give to the sensations that we perceive. Light that has a wavelength of 570 nm, for example, stimulates “red” and “green” cones about equally, and we “see” yellow. That’s why we say that R+G=Y. That’s why we also say that 570 nm light is “yellow” light.
Extra spectral colors are colors that don’t correspond to any one single wavelength of light. They are “real” colors, in the sense that retinal cones get stimulated and our brains perceive something. However, extra spectral colors don’t appear in any rainbow. To make an extra spectral color, more than one wavelength of light must hit our retinas. Our brains then take this data and “create” the color we perceive.
In terms of the RGB color code, extra spectral colors are those in which both R and B (corresponding to the cones at either end of the visible spectrum) are non-zero. And I don’t know about you, but I have a very heavy preference against extra spectral colors.
Now, admittedly, white (RGB = [255,255,255]) is about as extra spectral as you can get. Does white annoy me? Not really; but as a color, it’s also pretty dull. Does anyone paint their bedroom pure white on purpose? Does anyone really want an entirely white car?
But the other extra spectral colors I mentioned earlier are a who’s who of mediocrity. Does anyone older than 16 actually like pink? Has anyone in the history of the world every uttered the sentence, “Gray is my favorite color”? And beige—ugh. Just, ugh.
Standard pink has an RGB code of [255, 192, 203]. Surprisingly, there are combinations that are much, much worse. Hot pink [255, 105, 180] disturbs me. Champagne pink [241, 221, 207] bothers me. Congo pink [248, 131, 121] doesn’t actually make your eyes bleed, but I had to check a mirror to verify this for myself.
Beiges are less offensive, but that’s like saying cauliflower tastes better than broccoli. Of particular note are “mode beige” [150, 113, 23] which used to be called “drab” but was re-branded in Orwellian fashion, and feldgrau [77, 93, 83] which was used in World War II by the German army, in an apparent attempt to win the war by losing the fashion battle.
This is speculation, but I’ve often wondered if these colors bother me because they are stimulating all three kinds of cones in my retina. Maybe in some deep part of the reptilian complex portion of my brain, I know (on an intuitive level) that these colors don’t correspond to any particular wavelength. These colors don’t appear in the rainbow. You can’t make a laser pointer with one of these colors. You can’t have a magenta, or a beige, or a gray photon. And somehow, my aesthetic sense knows this. So when I see the color “dust storm” [229, 204, 201] my limbic system tells me to wince, and I’m saved from even having to know why.
Anyway, I’d be interested in seeing which color(s) bother you the most. I’m going to guess the color(s) are extra spectral.
[Note: my book Why Is There Anything? is now available for download on the Kindle!]
Posted in Physics | Tagged beige, colors, extra spectral colors, feldgrau, pink, science | 14 Comments »
My wife called me the other day and asked what my favorite color was.
“Hold on one second,” I said. “I have it written down.”
She explained that she just needed a color in the most general terms, because she was buying me a case for my new iPhone. So I said “blue.” But I was disappointed that I didn’t get to be more specific.
You see, my actual favorite color is (currently) Tropical Rain Forest, formulated by Crayola in 1993. Its RGB color code is (0, 117, 94). If you want to read about the color, it’s the first variation on jungle green in the Wikipedia article of the same name.
But what’s an RGB color code? Anyone familiar with computer graphics will recognize RGB as standing for Red/Green/Blue, which are taken to be the three primaries. And therein lies a tale: for didn’t we all learn in kindergarten that red, blue, and yellow (not green) were the primary colors? What’s going on?
Light comes in different wavelengths, or more commonly, combinations of multiple wavelengths. Color is a purely biological phenomenon having to do with what we perceive with our eyes. So when a kindergarten teacher says that “mixing red and blue make purple”, there’s really a whole lot of physics and biology that’s being glossed over.
In our retinas, we (generally) have three kinds of cones that react to incoming light. These cones can detect many wavelengths of light, but each peaks in a different part of the spectrum. Very simplistically, we can say that one peaks in the “red” part of the visible spectrum, one peaks in the “green” part of the spectrum, and one peaks in the “blue”.
Now, the “red” cones don’t just react to red light—it’s just that they react most strongly to red light. But light in the “green” part of the spectrum might also stimulate a “red” cone to some degree. The colors that we see depend on how our brains interpret three signals: how much each of the three kinds of cones is stimulated by incoming wavelengths of light. For example, if a “red” cone and a “green” cone were stimulated about equally, your brain would interpret this as seeing yellow. If all three cones were stimulated strongly, you’d “see” white. (It’s weird to note that different combinations of wavelengths can actually cause the same sensation in your brain: there’s not necessarily a unique combination of wavelengths for any given color perceived.)
Here’s a chart to help you out (note that this is very simplistic and glosses over many issues which I will address later):
Kind(s) of cone stimulated What you perceive
“Red” Red
“Green” Green
“Blue” Blue
Red & Green Yellow
Red & Blue Magenta
Green & Blue Cyan
Looking at this chart makes the notion of an “additive” primary easy to understand. We declare red, green, and blue (RGB) to be the additive primary colors. We can then build (most) other colors by adding these colors together. This corresponds to multiple wavelengths of light stimulating one or more cones in the retina to varying degrees. If you want an applet to play around with this kind of additive color mixing, try this. Input (0, 117, 94) if you want to see Tropical Rain Forest.
One caveat: the RGB scheme arbitrarily chooses three exact wavelengths of light to be “the” additive primaries, but this represents a judgment call on our part. The degree to which different wavelengths of light stimulate the three kinds of cones is messy; the graphs of intensity (of cone response) vs. wavelength are not perfect bell curves, and have bumps and ridges. Furthermore, it has long been known that if you try to limit yourself to only three “primary” additive colors then you cannot reproduce every possible color that humans can perceive. We would say that the gamut of possible colors you can make with an RGB scheme does not encompass all possible perceived colors. (For example, true violet as seen in the rainbow cannot be reproduced with RGB—it can only be approximated. You can’t see true violet on a computer monitor!)
Now, tell a 6-year-old that Red + Green = Yellow, and they will look at you like you’ve grown a second head. That’s because most experience we have with “color mixing” doesn’t involve mixing different kinds of light; it involves mixing different kinds of pigments. And that’s a totally different ball of (crayon?) wax.
Suppose I have a flashlight that shines red light. I have another flashlight that shines green light. If I shine both flashlights into your eyes, you will see yellow, as we just discussed. With two flashlights (two colors), more light has reached your eyes than would have with just one flashlight.
Pigments (such as crayons or paint) work in the opposite way. “Red” paint is paint that takes white light (a combination of R,G, and B) and subtracts some of the light away, so that only the R reaches your eyes. Green paint takes RGB light and lets only the G reach your eyes. In other words, red paint “blocks” G and B, whereas green paint “blocks” R and B.
Can you guess what happens if we mix red and green paint?
The 6-year-old knows you get black. That’s because two successive blockers have filtered out all the light, and nothing reaches your eyes at all. And when no cones are stimulated, we perceive that as black.
When a teacher says that the “primary” colors are red, blue, and yellow, they are referring to so-called subtractive primaries. By mixing those three kinds of pigments, you can make many of the colors we can see. But not all the colors. Try mixing red, blue, and yellow to make pink. It cannot be done. Like the additive primaries, the gamut of the subtractive primaries is limited. And, like the choice of RGB as additive primaries, the choice of red, blue, and yellow as the subtractive primaries is arbitrary. Arbitrary, and inferior. It turns out that using yellow, magenta, and cyan as the subtractive primaries expands the gamut and increases the number of colors you can make by subtraction.
Why yellow, magenta, and cyan? Well, those choices make sense if you’ve already picked RGB as your additive primaries. Consider the chart above. It’s clear that a paint that looks magenta must be blocking green, since you’re seeing an (additive) combination of red and blue. Similarly, yellow paint blocks blue, and cyan paint blocks red. So what happens if we mix, say, yellow and cyan? Well, the mixture will block blue, and then block red, so what is left is green. You can try this here.
Anyway, I spent some time at this site trying to determine exactly my favorite color. I finally chose Tropical Rain Forest, RGB=(0, 117, 94). I think it’s peaceful and organic. I also enjoy Tyrian purple, RGB = (102, 2, 60). Let me know which colors you favor.
Coming soon: some thoughts about the extra-spectral colors!
Posted in Physics | Tagged color, Crayola, Physics, RGB, rgb color code, science, Tropical Rain Forest, wavelengths of light | 9 Comments »
A friend of mine recently made the following challenge: can you start a story with one sentence, and logically end with another sentence? The sentences were:
(1) The washing machine repairman grunted.
(2) The archbishop vowed never to eat figs again.
In the spirit of Oulipo (Ouvroir de littérature potentielle) I present my efforts here. Don’t forget : if you’re a many-worlds adherent, then this is a true story.
The Foundation that Saves
The washing machine repairman grunted. “I don’t know as you remember as much of the Bible as you think, your Excellency.” He wiped his hands on his boilersuit.
“You may be right. But still—can the Bendix be saved?”
“Well sir, that’s what I was referrin’ to. Saving. This here contraption, it wobbles a great bit, drifts, if you will. So if’n you need it to stop walkin’ across the floor, well sir, it needs a foundation, like.” His eyes glittered.
Lang nodded. “I get your reference now. You said the machine couldn’t be shaken by the steam if it were founded upon a rock. That’s what, Luke Chapter 6?”
“Just so, your Excellency. When the steam from the intake beats vehemently, well sir, the pantry here gets a might flooded, with all your Canterbury particulars and vestments getting wet and so forth. ‘less of course we was to bolt the ol’ Bendix to the floor so as it didn’t walk. And so I thought of my Sunday canon, sir, and heard my ol’ rector saying clear as a bell: ‘He is like a man which built an house, and digged deep, and laid the foundation on a rock: and when the flood arose, the stream beat vehemently upon that house, and could not shake it: for it was founded upon a rock’.”
“I am impressed.”
“As long as you ain’t impressed by no rock, sir, then we’re good, sir, if you get my meaning.”
Lang smiled. “You have a deep knowledge of scripture, for—”
“You can say it, Excellency. For a handyman. My mum raised me proper, in the ecclesia anglicana if you will, sir.”
“And you were saying, I don’t remember as much of the Bible as I might think I do.”
Mr. Suttles stood up, cracking his knuckles and turning to face Archbishop Cosmo Lang. “Well, you was talkin’ about the Lady’s feast upstairs, the bounty, how it was ‘a land of wheat, and barley, and vines, and fig trees, and pomegranates; a land of olive oil, and honey’.”
“Deuteronomy 8:8.”
“But our Lord Jesus didn’t go in for any figs, you understand, despite what the Old Testament might say.”
The archbishop smiled. “You refer to Mark Chapter 11. When our Lord comes across the fig tree, and finds it barren—”
“Yes, sir. With all respect, Excellency, Jesus forbade us to eat figs ever again, and I for one don’t want to disobey.”
“Well, it was a parable, son. The point was that—”
“Plus, them figs that grow on Dr. Speelman’s farm, well sir, they’re infested. Wasps, you know. They lay their eggs in the figs, and them larvae hatch inside, and eat up the seeds, sir, and get right fat and happy. You ever bite into a fig, sir, and feel that crunchy, gritty texture? Like them little globules that get stuck in your teeth, kinda soft yet kinda firm at the same time? They as get stuck like that, are wasp eggs. I kid you not, Excellency. Jesus knew what he was talking about. He didn’t want to eat no wasp eggs, and didn’t want his disciples eating no wasp eggs, neither. That’s one foundation I can get behind. So forget about no land of bounty with wheat and honey and figs. Stay away from those larvae.”
The archbishop vowed never to eat figs again.
Posted in Uncategorized | Tagged figs, Jesus, many-worlds, Oulipo, wasps | 2 Comments »